MATHS WORLD

Quadrilaterals:

You will study here . . .

1. Sum of the angles of a quadrilateral is 360°.

2. A diagonal of a parallelogram divides it into two congruent triangles.
3. In a parallelogram,

(i) opposite sides are equal

(ii) opposite angles are equal

(iii)diagonals bisect each other

4.A quadrilateral is a parallelogram, if

(i)opposite sides are equal

or (ii) opposite angles are equal

or (iii) diagonals bisect each other

or (iv)a pair of opposite sides is equal and parallel

5. Diagonals of a rectangle bisect each other and are equal and vice-versa.
6. Diagonals of a rhombus bisect each other at right angles and vice-versa.
7. Diagonals of a square bisect each other at right angles and are equal, and vice-versa.
8. The line-segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it.

9. A line through the mid-point of a side of a triangle parallel to another side bisects the third side.

10. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral, in order, is a parallelogram

You have studied many properties of a parallelogram in this chapter and you have also verified that if in a quadrilateral any one of those properties is satisfied, then it becomes a parallelogram.

We now study yet another condition which is the least required condition for a quadrilateral to be a parallelogram.

It is stated in the form of a theorem as given below:

Theorem 1: A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.

Look at Fig 8.17 in which AB = CD and AB || CD. Let us draw a diagonal AC. You can show that∆ ABC≅∆ CDA by SAS congruence rule.

So, BC || AD (Why?)

Let us now take an example to apply this property of a parallelogram.

Example 6: ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD

(See Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that:
(i) APCQ is a parallelogram.
(ii)DPBQ is a parallelogram.
(iii)PSQR is a parallelogram

The Mid-point Theorem

You have studied many properties of a triangle as well as a quadrilateral. Now let us study yet another result which is related to the mid-point of sides of a triangle. Perform the following activity.

Draw a triangle and mark the mid-points E and F of two sides of the triangle. Join the points E and F (see Fig. 8.24).

Measure EF and B. Measure ∠ AEF and ∠ ABC.

You will find that:

EF =12BC and∠ AEF =∠ ABC

So, EF || BC

Repeat this activity with some more triangles.

So, we arrive at the following theorem:

Theorem 2: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.

You can prove this theorem using the following

Clue: Observe Fig 8.25 in which E and F are mid-points of AB and AC respectively and CD || BA.

∆AEF ≅∆ CDF (ASA Rule)

So,

EF = DF and BE= AE = DC Therefore, BCDE is a parallelogram. (Why?)This gives EF || BC.

In this case, also note that EF =12ED = 12BC

Theorem 3: The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side

In Fig 8.26, observe that E is the mid-point of AB, line l is passing through E and is parallel to BC and CM || BA.

Prove that AF = CF by using the congruence of

∆AEF and ∆CDF.

Theorem 4: The diagonals of a parallelogram bisect each other.

Theorem 5: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.

You can reason out this result as follows:

Note that in Fig. 8.11, it is given that OA = OC and OB = OD.

So,

∆AOB ≅∆COD (Why?)

Therefore, ∠ ABO =∠ CDO (Why?)

From this, we get AB || CD

Similarly,

BC || AD

Therefore ABCD is a parallelogram

Theorem 6: If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.

Can you reason out why?

Let sides AB and CD of the quadrilateral ABCD be equal and also AD = BC (see Fig. 8.9). Draw a diagonal AC.

Clearly,

∆ABC ≅∆CDA

(Why?)

So,

∠BAC = ∠DCA and

∠BCA = ∠DAC

(Why?)

Can you now say that ABCD is a parallelogram? Why?

Theorem 7: In a parallelogram, opposite angles are equal.

Theorem 8: If in a quadrilateral, each pair of opposite angles is equal, then

It is a parallelogram.

Areas of parallelograms and triangles:

You will study here:

In this chapter, you have studied the following points:

1. Area of a figure is a number (in some unit) associated with the part of the plane enclosed by that figure.

2. Two congruent figures have equal areas but the converse need not be true.

3. If a planar region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T) = ar (P) + ar (Q), where ar (X) denotes the area of figure X.

4. Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices, (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.

5. Parallelograms on the same base (or equal bases) and between the same parallels are equal in area.

6. Area of a parallelogram is the product of its base and the corresponding altitude.

7. Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels.

8. If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.

9. Triangles on the same base (or equal bases) and between the same parallels are equal in area.

10. Area of a triangle is half the product of its base and the corresponding altitude.

11. Triangles on the same base (or equal bases) and having equal areas lie between the same parallels.

12. A median of a triangle divides it into two triangles of equal areas. Look at the following figures:

(i), trapezium ABCD and parallelogram EFCD have a common side DC. We say that trapezium ABCD and parallelogram EFCD are on the same base DC. Similarly, in Fig. 9.4 (ii), parallelograms PQRS and MNRS are on the same base SR; in Fig. 9.4(iii), triangles ABC and DBC are on the same base BC and in Fig. 9.4(iv), parallelogram ABCD and triangle PDC are on the same base DC.

Now look at the following figures:

In Fig. 9.5(i), clearly trapezium ABCD and parallelogram EFCD are on the same base DC. In addition to the above, the vertices A and B (of trapezium ABCD) opposite

To base DC and the vertices E and F (of parallelogram EFCD) opposite to base DC lie on a line AF parallel to DC. We say that trapezium ABCD and parallelogram EFCD are on the same base DC and between the same parallels AF and DC. Similarly, parallelograms PQRS and MNRS are on the same base SR and between the same parallels PN and SR [see Fig.9.5 (ii)] as vertices P and Q of PQRS and vertices M and N of MNRS lie on a line PN parallel to base SR. In the same way, triangles ABC and DBC lie on the same base BC and between the same parallels AD and BC [see Fig. 9.5 (iii)] and parallelogram ABCD and triangle PCD lie on the same base DC and between the same parallels AP and DC

So, two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base. Keeping in view the above statement, you cannot say that ∆PQR and ∆DQR of (i) lie between the same parallels and QR. Similarly, you cannot say that parallelograms EFGH and MNGH lie between the same parallels EF and HG and that parallelograms ABCD and EFCD of lie between the same parallels AB and DC (even though they have a common base DC and lie between the parallels AD and BC). So, it should clearly be noted that out of the two parallels, one must be the line containing the common base. Note that ∆ABC and ∆DBE of Fig. are not on the common base. Similarly, ∆ABC and parallelogram PQRS of are also not on the same base.

9.3 Parallelograms on the same Base and Between the same Parallels

Now let us try to find a relation, if any, between the areas of two parallelograms on thesame base and between the same parallels. For this, let us perform the following activities:

Let us take a graph sheet and draw two parallelograms ABCD and

PQCD on it as shown in the figure.

The above two parallelograms are on the same base DC and between the same parallels PB and DC. You may recall the method of finding the areas of these two parallelograms by counting the squares.

In this method, the area is found by counting the number of complete squares enclosed by the figure, the number of squares a having more than half their parts enclosed by the figure and the number of squares having half their parts enclosed by the figure. The squares whose less than half parts are enclosed by the figure are ignored. You will find that areas of both the parallelograms are (approximately) 15cm2.Repeat this activity* by drawing some more pairs of parallelograms on the graph sheet. What do you observe? Are the areas of the two parallelograms different or equal? If fact, they are equal. So, this may lead you to conclude that parallelograms on the same base and between the same parallels are equal in area. However, remember that this is just verification.

Theorem 1: Parallelograms on the same base and between the same parallels are equal in area.

Proof: Two parallelograms ABCD and EFCD, on the same base DC and between the same parallels

AF and DC are given (see Fig.9.12).

We need to prove that ar (ABCD) = ar (EFCD).

In ∆ADE and ∆BCF,

∠DAE = ∠CBF (Corresponding angles from AD || BC and transversal AF)

(1)

∠AED = ∠BFC (Corresponding angles from ED || FC and transversal AF)

(2)

Therefore, ∠ADE = ∠BCF (Angle sum property of a triangle)

(3)

Also,

AD = BC (Opposite sides of the parallelogram ABCD)

(4)

So,

∆ADE≅ ∆BCF

[By ASA rule, using (1), (3), and (4)]

Therefore, ar (ADE) = ar (BCF) (Congruent figures have equal areas)

(5)

Now, ar (ABCD) = ar (ADE) + ar (EDCB)

= ar (BCF) + ar (EDCB)

[From (5)]

= ar (EFCD)

So, parallelograms ABCD and EFCD are equal in area.

Let us now take some examples to illustrate the use of the above theorem.

Example 1: In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle.

Also, AL ⊥DC. Prove that (i) ar (ABCD) = ar (EFCD)(ii) ar (ABCD) = DC × AL

Solution: (i) As a rectangle is also a parallelogram, therefore,

ar (ABCD) = ar (EFCD)

(Theorem 9.1)

(ii) From above result,

ar (ABCD) = DC × FC (Area of the rectangle = length × breadth)(1)

AL⊥DC, therefore, AFCL is also a rectangle

So,

AL = FC

(2)

Therefore, ar (ABCD) = DC × AL

[From (1) and (2)]

Can you see from the Result (ii) above that area of a parallelogram is the product of its any side and the corresponding altitude? Do you remember that you have studied this formula for area of a parallelogram in Class VII? On the basis of this formula, Theorem 9.1 can be rewritten as parallelograms on the same base or equal bases and between the same parallels are equal in area.

Can you write the converse of the above statement? It is as follows: Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels. Is the converse true? Prove the converse using the formula for area of the parallelogram.

Example 2: If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.

Solution: Let ∆ABP and parallelogram ABCD be on the same base AB and between the same parallels

AB and PC (see Fig. 9.14).

You wish to prove that ar (PAB) =1ar (ABCD)

Draw BQ || AP to obtain another parallelogram ABQP. Now parallelograms ABQP and ABCD are on the same base AB and between the same parallels AB and PC.

Therefore,

ar (ABQP) = ar (ABCD)

(By Theorem 9.1)

But ∆PA B ≅ ∆BQP (Diagonal PB divides parallelogram ABQP into two congruent triangles.) (1)

So,

ar (PAB) = ar (BQP)

(2)

Therefore,

ar (PAB) =12ar (ABQP) [From (2)]

(3)

This gives

ar (PAB) =1ar (ABCD)

[From (1) and (3)].

9.4 Triangles on the same Base and between the same Parallels

Let us look at Fig. 9.18. In it, you have two triangles ABC and PBC on the same base BC and between the same parallels BC and AP. What can you say about the areas of such triangles? To answer this question, you may perform the activity of drawing several pairs of triangles on the same base and between the same parallels on the graph sheet and find their areas by the method of counting the squares. Each time, you will find that the areas of the two triangles are (approximately) equal. This activity can be performed using a geoboard also. You will again find that the two areas are (approximately) equal.

To obtain a logical answer to the above question,

you may proceed as follows:

Draw CD || BA and CR || BP such that D and R lie on line AP

From this, you obtain two parallelograms PBCR and ABCD on the same base BC and between the same parallels BC and AR.

Therefore,

ar (ABCD) = ar (PBCR)(Why?)

Now

∆ABC≅ ∆CDA and ∆PBC≅ ∆CRP (Why?)

So,

ar (ABC) =1ar (ABCD)

and ar (PBC) =1ar (PBCR)

(Why?)

Therefore,

ar (ABC) = ar (PBC)

In this way, you have arrived at the following theorem:

Theorem 2: Two triangles on the same base (or equal bases) and between the

same parallels are equal in area.

Now, suppose ABCD is a parallelogram whose one of the diagonals is AC

Let AN⊥DC. Note that

∆ADC≅ ∆CBA

(Why?)

So,

ar (ADC) = ar (CBA)

(Why?)

Therefore,

ar (ADC) =1ar (ABCD)

=1(DC AN)

(Why?)

So, area of ∆ADC =12 × base DC × corresponding altitude AN

In other words, area of a triangle is half the product of its base (or any side) and

the corresponding altitude (or height). Do you remember that you have learnt this formula for area of a triangle in Class VII? From this formula, you can see that two

triangles with same base (or equal bases) and equal areas will have equal corresponding altitudes.

For having equal corresponding altitudes, the triangles must lie between the same parallels. From this, you arrive at the following converse of Theorem 2.

Theorem 3: Two triangles having the same base (or equal bases) and equal

areas lie between the same parallels.

Let us now take some examples to illustrate the use of the above results.

Example 3: Show that a median of a triangle divides it into two triangles of equal areas.

Solution: Let ABC be a triangle and let AD be one of its medians

(see Fig. 9.21).

You wish to show that

ar (ABD) = ar (ACD).

Since the formula for area involves altitude, let us

draw AN⊥BC.

Now

ar(ABD) =12× base × altitude (of∆ ABD)

=1BD AN x 2

Example 4 : In Fig. 9.22, ABCD is a quadrilateral

and BE || AC and also BE meets DC produced at E.

Show that area of ∆ADE is equal to the area of the

quadrilateral ABCD.

Solution : Observe the figure carefully .

∆BAC and ∆EAC lie on the same base AC and

between the same parallels AC and BE.

Therefore,

ar(BAC) = ar(EAC)

(By Theorem 2)

So, ar(BAC)+ar(ADC)=ar(EAC) + ar(ADC)(Adding same areas on both sides) or

ar(ABCD) = ar(ADE)

Circle:

You will learn :

In this chapter, you will study the following points:

1.A circle is the collection of all points in a plane, which are equidistant from a fixed point in

the plane.

2.Equal chords of a circle (or of congruent circles) subtend equal angles at the centre.

3.If the angles subtended by two chords of a circle (or of congruent circles) at the centre

(corresponding centres) are equal, the chords are equal.

4.The perpendicular from the centre of a circle to a chord bisects the chord.

5.The line drawn through the centre of a circle to bisect a chord is perpendicular to the

chord.

6.There is one and only one circle passing through three non-collinear points.

7.Equal chords of a circle (or of congruent circles) are equidistant from the centre (or

corresponding centres).

8.Chords equidistant from the centre (or corresponding centres) of a circle (or of congruent circles) are equal.

9.If two arcs of a circle are congruent, then their corresponding chords are equal and conversely if two chords of a circle are equal, then their corresponding arcs (minor, major) are congruent.

10.Congruent arcs of a circle subtend equal angles at the centre.

11.The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

12.Angles in the same segment of a circle are equal.
13.Angle in a semicircle is a right angle.
14.If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle.

15.The sum of either pair of opposite angles of a cyclic quadrilateral is 1800.

16.If sum of a pair of opposite angles of a quadrilateral is 1800, the quadrilateral is cyclic.

Theoram 1: Equal chords of a circle subtend equal angles at the centre.

Proof : You are given two equal chords AB and CD

of a circle with centre O (see Fig.10.13). You want

to prove that∠ AOB =∠ COD.

In triangles AOB and COD,

OA = OC

(Radii of a circle) OB = OD (Radii of a circle) AB = CD

(Given)

Therefore,

∆AOB ≅ ∆C O D

(SSS rule)

This gives

∠AOB = ∠C O D

(Corresponding parts of congruent triangles)

Theorem 2 : If the angles subtended by the chords of a circle at the centre

are equal, then the chords are equal.

The above theorem is the converse of the Theorem 10.1. Note that in Fig. 10.13,

if you take∠ AOB =∠ COD, then

∆AOB ≅ ∆ COD

Theorem 3 : The perpendicular from the centre of a circle to a chord bisects

the chord.

Theorem 4 : The line drawn through the centre of a circle to bisect a chord is

perpendicular to the chord.

Is this true? Try it for few cases and see. You will see that it is true for these cases. See if it is true, in general, by doing the following exercise. We will write the stages and you give the reasons.

Let AB be a chord of a circle with centre O and O is joined to the mid-point M of AB. You have to prove that OM⊥ AB. Join OA and OB. In triangles OAM and OBM,

OA = OB

AM = BM

OM = OM (Common)

Therefore,∆OAM≅ ∆OBM

This gives∠OMA =∠OMB = 90°

Theorem 5 :T h e re is one and only one circle passing through three given

non-collinear points

Theorem 6 : Equal chords of a circle(or of congruent circles) are equidistant

from the centre(or centres)

Theorem 7 :C h o rds equidistant from the centre of a circle are equal in

length.

Example 2 : If two intersecting chords of a circle make equal angles with the diameter

passing through their point of intersection, prove that the chords are equal.

Solution : Given that AB and CD are two chords of

a circle, with centre O intersecting at a point E. PQ is a diameter through E, such that∠ AEQ=∠ DEQ (see Fig.10.24). You have to prove that AB = CD. Draw perpendiculars OL and OM on chords AB and CD respectively. Now

∠LOE = 180° – 90° – ∠LEO = 90° – ∠LEO

(Angle sum property of a triangle)
= 90° –∠ AEQ = 90° –∠ DEQ
= 90° –∠ MEO =∠ MOE

In triangles OLE and OME,

∠ LEO = ∠MEO

∠ LOE = ∠MOE (Proved above)

EO = EO (Common)

Therefore,

∆O L E ≅ ∆OME

This gives:

OL = OM (CPCT)

So,

AB = CD

Theorem 8 : The angle subtended by an arc at the centre is double the angle

subtended by it at any point on the remaining part of the circle.

Proof : Given an arc PQ of a circle subtending angles POQ at the centre O and

PAQ at a point A on the remaining part of the circle. We need to prove that

∠POQ = 2 ∠PAQ.

Fig. 10.28

Consider the three different cases as given in Fig. 10.28. In (i), arc PQ is minor; in (ii),

arc PQ is a semicircle and in (iii), arc PQ is major.

Let us begin by joining AO and extending it to a point B.

In all the cases,

∠BOQ = ∠OAQ + ∠AQO

because an exterior angle of a triangle is equal to the sum of the two interior opposite angles.

Also in∆ OAQ,

OA = OQ (Radii of a circle)

Therefore,

∠OAQ = ∠OQA (Theorem 7.5)

This gives

∠BOQ = 2 ∠O A Q (1)

Similarly,

∠BOP = 2 ∠O A P

(2)

From (1) and (2),∠ BOP +∠ BOQ = 2(∠ OAP +∠ OAQ)

This is the same as

∠POQ = 2 ∠ PAQ

(3)

For the case (iii), where PQ is the major arc, (3) is replaced by

reflex angle POQ = 2∠ PAQ

Theorem 9 : Angles in the same segment of a circle are equal.

Again let us discuss the case (ii) of Theorem 10.8 separately. Here∠PAQ is an angle

in the segment, which is a semicircle. Also,∠ PAQ =12∠POQ =12× 180° = 90°.

If you take any other point C on the semicircle, again you get that

∠ PCQ = 90°

Therefore, you find another property of the circle as:

Angle in a semicircle is a right angle.

The converse of Theorem 10.9 is also true. It can be stated as:

Theorem 10 : If a line segment joining two points subtends equal angles at

two other points lying on the same side of the line containing the line segment,

the four points lie on a circle(i.e. they are concyclic)

Theorem 11 : The sum of either pair of opposite angles of a cyclic

quadrilateral is1 8 0 º .

In fact, the converse of this theorem, which is stated below is also true.

Theorem 12 : If the sum of a pair of opposite angles of a quadrilateral is

180º, the quadrilateral is cyclic.

Example 3 : In Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to the

radius of the circle. AC and BD when extended intersect at a point E. Prove that

∠AEB = 60°.

Solution : Join OC, OD and BC.

Triangle ODC is equilateral

Therefore,∠ COD = 60°

Now,

∠CBD =12∠COD (Theorem 10.8)

This gives

∠ CBD = 30°

Again,

∠ ACB = 90°

So,

∠BCE = 180° – ∠ACB = 90°

Which gives∠ CEB = 90° – 30° = 60°, i.e.∠ AEB = 60°

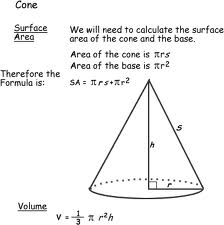
Surface Areas and Volumes

In this chapter, you will read:

1. Surface area of a cuboid = 2 (lb +bh +hl)

2. Surface area of a cube = 6a2

3. Curved surface area of a cylinder = 2πrh

4. Total surface area of a cylinder = 2π r(r+ h)

5. Curved surface area of a cone = πrl

6. Total surface area of a right circular cone =π r(l+ r)

7. Surface area of a sphere of radius r = 4πr2

8. Curved surface area of a hemisphere = 2πr2

9. Total surface area of a hemisphere = 3π r2

10. Volume of a cuboid =l ×b ×h

11. Volume of a cube =a3

12. Volume of a cylinder = πr2h

13. Volume of a cone =1/3πr2h

14. Volume of a sphere of radius =4/3*r3

15. Volume of a hemisphere =2/3 πr3

Example1 :A wall of length 10 m was to be built across an open ground. The height

of the wall is 4 m and thickness of the wall is 24 cm. If this wall is to be built up with bricks whose dimensions are 24 cm × 12 cm × 8 cm, how many bricks would be required?

Solution 1: Since the wall with all its bricks makes up the space occupied by it, we

need to find the volume of the wall, which is nothing but a cuboid.

Here,

Length =10 m = 1000 cm

Thickness =24 cm

Height =4 m = 400 cm

Therefore,

Volume of the wall =length × thickness × height

=1000 × 24 × 400 cm3
Now, each brick is a cuboid with length = 24 cm, breadth = 12 cm and height = 8 cm
So, volume of each brick = length × breadth × height

= 24 × 12 × 8 cm3

So, number of bricks required=volume of the wall

volume of each brick

=1000 × 24 × 400

24 × 12 × 8

= 4166.6

So, the wall requires 4167 bricks

REMARK: π is an irrational number. So, the value of π is a non-terminating, non-repeating decimal. But when we use its value in our calculations, we usually take its value as approximately equal to 22/7 or 3.14.

STATISTICS

In this chapter, you will study the following points:

1. Facts or figures, collected with a definite purpose, are called data.

2. Statistics is the area of study dealing with the presentation, analysis and interpretation of data.

3. How data can be presented graphically in the form of bar graphs, histograms and frequency polygons.

4. The three measures of central tendency for ungrouped data are:

(i) Mean: It is found by adding all the values of the observations and dividing it by the total number of observations. It is denoted by x .

For an ungrouped frequency distribution, it is x =

(ii)Median: It is the value of the middle-most observation (s).

If n is an even number, median = Mean of the values of the2n

(iii)Mode: The mode is the most frequently occurring observation.

Let us consider an example.

Example 9 : In a city, the weekly observations made in a study on the cost of living

index is given in the following table:

Cost of living index Number of weeks

140 – 150 5

150 – 160 10

160 – 170 20

170 – 180 9

180 – 190 6

190 – 200 2

Total 52

Draw a frequency polygon for the data above (without constructing a histogram).

Solution : Since we want to draw a frequency polygon without a histogram, let us find

the class-marks of the classes given above, that is of 140 - 150, 150 - 160,....

For 140 - 150, the upper limit = 150, and the lower limit = 140

So, the class-mark =150 + 140/2 =290/2 = 145.

PROBABILITY

WHAT WILL YOU LEARN HERE :

In this chapter, you will study the following points:

1. An event for an experiment is the collection of some outcomes of the experiment.

2. The empirical (or experimental) probability P(E) of an event E is given by P(E) = number of trials in which E has happened / Total number of trials.

3. The Probability of an event lies between 0 and 1
(NOTE:Please refer to NCERT mathematics book class 9 for images of examples)
here are some tricks related to mathematics.....go to the link and you can even surprise your friends after showing these tricks!!

http://freestylemind.com/mental-math-tricks

--------------------------------------------------------------------------------OOoo....

MATHS WORLD

Friday, February 11, 2011

Tuesday, February 8, 2011

HISTORY OF MATHS !!!

History of mathematics

Quadrilateral

Areas of Parallelograms and Triangles

Circles

Constructions

Statistics

Probability

HISTORY OF MATHEMATICS

CHAPTERS !!!