CONTENTS

History of mathematics

Quadrilateral

ü Introduction

ü Angle Sum Property of a Quadrilateral

ü Types of Quadrilaterals

ü Properties of a Parallelogram

ü Another Condition for a Quadrilateral to be a Parallelogram

ü The Mid-point Theorem

ü Summary

Areas of Parallelograms and Triangles

ü Introduction

ü Figures on the same Base and between the same Parallels

ü Parallelograms on the same Base and

ü Between the same Parallels

ü Triangles on the same Base and between

ü The same Parallels

ü Summary

Circles

ü Introduction

ü Circles and its Related Terms: A Review

ü Angle Subtended by a Chord at a Point

ü Perpendicular from the Centre to a Chord

ü Circle through Three Points

ü Equal Chords and their Distances from the Centre

ü Angle Subtended by an Arc of a Circle

ü Cyclic Quadrilaterals

ü Summary

Constructions

ü Introduction

ü Basic Constructions

ü Some Constructions of Triangles

ü Summary

Surface Areas and Volumes

ü Introduction

ü Surface Area of a Cuboid and a Cube

ü Surface Area of a Right Circular Cylinder

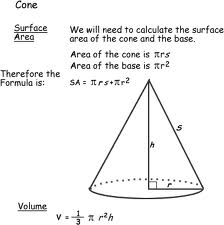
ü Surface Area of a Right Circular Cone

ü Surface Area of a Sphere

ü Volume of a Cuboid

ü Volume of a Cylinder

ü Volume of a Right Circular Cone

ü Volume of a Sphere

ü Summary

Statistics

ü Introduction

ü Collection of Data

ü Presentation of Data

ü Geographical Representation of Data

ü Measures of Central Tendency

ü Summary

Probability

ü Introduction

ü Probability – an Experimental Approach

ü Summary

HISTORY OF MATHEMATICS

Mathematics as a formal area of teaching and learning was developed about 5,000 years ago by the Sumerians. They did this at the same time as they developed reading and writing. However, the roots of mathematics go back much more than 5,000 years.

Throughout their history, humans have faced the need to measure and communicate about time, quantity, and distance. The Ishango Bone is a bone tool handle approximately 20,000 years old.

The picture given below shows Sumerian clay tokens whose use began about 11,000 years ago. Such clay tokens were a predecessor to reading, writing, and mathematics.

The development of reading, writing, and formal mathematics 5,000 years ago allowed the codification of math knowledge, formal instruction in mathematics, and began a steady accumulation of mathematical knowledge.

Mathematics as a Discipline

A discipline (an organized, formal field of study) such as mathematics tends to be defined by the types of problems it addresses, the methods it uses to address these problems, and the results it has achieved. One way to organize this set of information is to divide it into the following three categories (of course, they overlap each other):

1. Mathematics as a human endeavor. For example, consider the math of measurement of time such as years, seasons, months, weeks, days, and so on. Or, consider the measurement of distance, and the different systems of distance measurement that developed throughout the world. Or, think about math in art, dance, and music. There is a rich history of human development of mathematics and mathematical uses in our modern society.

2. Mathematics as a discipline. You are familiar with lots of academic disciplines such as archeology, biology, chemistry, economics, history, psychology, sociology, and so on. Mathematics is a broad and deep discipline that is continuing to grow in breadth and depth. Nowadays, a Ph.D. research dissertation in mathematics is typically narrowly focused on definitions, theorems, and proofs related to a single problem in a narrow subfield in mathematics.

3. Mathematics as an interdisciplinary language and tool. Like reading and writing, math is an important component of learning and "doing" (using one's knowledge) in each academic discipline. Mathematics is such a useful language and tool that it is considered one of the "basics" in our formal educational system.